
Laws of thought are three simple rules that constitute the foundation of every thought process we ever do. Like any fundamental concept, they can neither be proven nor concluded from anything else. However, their negation (opposite, contrary) can be argued against very strongly. Three traditional laws date from as far back as the times of Plato and Aristotle, the famous Greek philosophers. Over the centuries, we came to a more proper understanding of these laws and how to use them. During the Renaissance in Europe, much development in sciences and philosophy took place. Gottfried Leibniz, the famous German polymath, revisited the laws of thought, and added to them, although some of his additions are still somewhat controversial. In this article, we discuss the laws of thought, their meaning, how to use them properly, and provide some examples for using them in mathematics. However, mathematical examples are not necessary for the understanding of the laws of thought or this discussion.
The laws of thought are at the core of our thought process. Everything we think of depends on proper use of these laws. The entire field of mathematics is built on a handful of fundamental, simple concepts; one of them is deductive reasoning, which is built on the laws of thought. Mathematics is a cornerstone of all modern sciences, because the scientific method necessitates quantification, which is impossible without mathematics. Therefore, all modern sciences would not have been existed without the laws of thought. Although the laws of thought seem pretty intuitive, they are very frequently used improperly; their proper use requires conscious effort. Some causes of the improper use are discussed herein.
This article is quite lengthy. For those who do not have the time or the interest to read everything, key concepts are illustrated in grey boxes with a picture of a key. They are placed near where the discussion of the concept is. You can skim through them and, if you are interested, read the discussions of the topics of interest. Illustrations are also provided to support the concept. Also, some technical mathematical discussions or examples are provided. These are also in grey boxes, but without the picture of a key. If you are not into mathematics, you can easily skip those.
- Law of identity
- Law of non-contradiction
- Law of the excluded middle
- Indiscernibility of the identicals and identity of the indiscernibles
- Meanings
- Monadic versus polyadic
- Identity of the indiscernibles revisited
- Extensional and intensional equivalence
- In everyday life
- In mathematics
- Principle of sufficient reason
First: Law of identity
A=A
A thing is itself!
This is a very simple and intuitive sentence, so much so that it almost makes no sense to emphasize it as a law. What could a thing be if not itself?! First, it is to be emphasized that the laws of thought speak about thoughts! Does this sound ridiculous?! It may not sound so when we re-think of what we mean by the law of identity. ‘A thing is itself’ refers to a concept, not a physical object. Every physical object that we know of has a corresponding concept in our minds, but not every concept in our minds has a corresponding physical object. When we mention the concept of freedom, we understand it, but no one can actually hold in their hands a physical object that is freedom. But even if one holds or sees something that is unrecognizable to them, they still have the concept of ‘unidentified object’ in their minds to represent it. The realm of though, therefore, encompasses the physical realm entirely, and it extends beyond it. What we mean by the law of identity is that concepts have to be defined accurately to avoid confusion that leads to wrong conclusions. Unlike the physical world, concepts can be shaped in any way we want, even in shapes that are impossible in the physical world. We can imagine whatever we want, even if we cannot see it or touch it. But we are prone to making mistakes when we think, because we are built for efficiency rather than accuracy.
The natural thought process
We tend to think ‘fast’ even if this means we are not thinking ‘accurately.’ Imagine that you are walking in the jungle, and that you saw what seemed to be a predator of some kind. The vast majority of people, if not the entirety of human beings in existence, would run away (that's unless they are there to fight the predator or something of that like.) They wouldn't stay and make sure that the situation is indeed dire, and that they need to run away. In doing so, they maximize their chances of survival. This still applies to us nowadays, even if the context is different. Imagine that you are walking in the street and you heard what seemed to be some kind of gunfire or explosion. The initial reaction of the vast majority of people is to duck, lie down, hide, or take cover of some sort, then curiosity might kick in, and they may or may not start to explore what is happening. They do not first investigate the source of what seems to be dangerous to determine accurately if it is indeed dangerous.
We tend to think in the big picture more than the details, especially when our well-being seems to be in danger.
Our natural thought process is built for efficiency, not for accuracy.
We also tend to make ‘shortcuts’ in our thought process in order to save resources. The most precious resource that we can never replace is time. Therefore, thinking fast is more important than thinking accurately. If our thought process is accurate enough we seem to be satisfied with what we conclude. Sometimes we are even strongly biased to what we conclude through such shortcuts that we wage little, personal wars to defend our beliefs. We tend to lose sight of this fact—that we are built for efficiency rather than precision—because it is so commonplace and seems to be hard-wired in our physical structure. And when we lose sight of it, we tend to get confused.
How many times have you heard about a police officer (or any armed person) who shot someone else because they thought they were armed and dangerous, but eventually turned out to be mistaken?! This, unfortunately, is not a rare occurrence. The shortcut they have in their mind at such time is ‘This person seems to carry a weapon; they seem to intend to use it; if they use it, I may get killed; I want to live; I have to stop them; I have a weapon myself; I can use my weapon to stop them; the law allows me to defend myself; even if I kill them in self-defense, I am not going to be punished; therefore, I will use my weapon to stop them, even if this means killing them.’ Of course no one in such situation would actually take the time to think about all of that. They simply react to the situation. This is good for survival, but results sometimes in terrible judgment. This kind of thinking is related to the logical fallacy called ‘the slippery slope fallacy;’ also used very frequently for fear mongering.
How many times in history can you identify incidents in which huge masses of people followed some fallacious beliefs just because the majority of people did so? The shortcut in this case is ‘People want to better themselves rather than to bring harm on themselves; the majority of people must be following this way of thinking; whatever they are doing must be good for them; I want good for myself; therefore, I will follow them.’ This kind of thinking is very common indeed, and it is the basis of a logical fallacy called ‘appeal to numbers,’ appeal to popularity, appeal to the masses, bandwagon fallacy, or argument by consensus. It is analogous to what happens in the animal world when enough of the herd starts running in a certain direction, and the rest of the herd follows. They follow passively, without knowing what they are running from or running into. The famous Asch conformity experiments and lots of variations of them provide evidence for the innate urge to conform to the majority. Running away from predators without waiting to verify the danger gives a better chance for survival; hence, that instinct is good for survival. However, lots of harm happened all along the history of humanity because of this instinct! The difference between animals and humans is that we can tame this instinct and subdue it to our minds. Following the crowds is useful in very limited situations, but quite useless and potentially harmful when it comes to fashion and propaganda. On the other hand, how many people in the history of science challenged the common beliefs of their time and thought innovatively? Very few indeed! So few that they constitute a tiny, negligible fraction of all those who worked in science. But those are the ones who brought about revolutionary changes in science by not following the crowds!
We are built for efficiency rather than precision, but we can override that default in the majority of situations and think with precision and accuracy. As a matter of fact, we should do that in as many situations as we can. But thinking accurately is hindered not only by the natural thought process, but also by natural languages.
Ambiguity of natural languages
you are not allowed to stop
doing anything at all?
Natural languages are those languages we have been using in everyday life to communicate with each other since the dawn of humanity. They evolved ‘naturally’ based on our thought process, with no special attention to rules or precision. Rules came later when languages started to mature, but some form was necessary for any language to facilitate its use. The primary aim of having a language is to facilitate communicating ideas between individuals. Therefore, a language has to be as efficient as possible. Humans have a limited ability to memorize, and languages require memorization of words. Therefore, efficient use of words means that we can use the same word in more than one way to express different things. The meanings of words depend on context and assumptions. It is easy to verify this. Open any dictionary of any natural language and see for yourself. You are highly unlikely to find a word that has one meaning only.
Context is a big determinants of how we understand words. Consider the word ‘light.’ In a context like ‘the sun shines its light,’ it is understood entirely differently than in a context like ‘this box is so light.’ Another example is the meaning of ‘fast’ in the context‘he is so fast’ versus the context ‘the fast starts tomorrow.’ Not only the linguistic context is a big determinant, but the situational context is, too, especially in verbal and confrontational communications. A lot of the meaning we understand is conveyed by nonverbal communication. Think of the possible meanings of the simple phrase ‘Go!’ in different situations. Said from a father to his son who was asking to go play with his friends, it has a totally different meaning than when it is said in a farewell situation or a heated argument! We use our languages also to express emotions.
Ambiguity is a characteristic of natural languages, which facilitates efficiency at the expense of precision and clarity.

Expressing emotions is not an easy task, because emotions are entirely subjective. We assume that others feel what we feel, but there is a lot of evidence that emotions varies between individuals, both quantitatively and qualitatively. The big challenge is to communicate something that only you feel to someone else. Hence, I believe, at least in part, idioms came to be. We use idioms to communicate concepts that have nothing to do with the actual literal meaning of words! We say “an apple to my eye” to express delight and gladness. We say “a rainy day” to express gloominess. Natural languages are anything but precise. A word has more than one meaning, and sometimes expressions have meanings that are not related to the literal meaning of words!
Furthermore, we assume that certain things are ‘impossible,’ and dismiss the idea completely based on that. Consider the expression ‘a school of fish.’ To almost all (if not truly all) of us, that expression is understood as ‘a group of fish swimming together.’ But there is nothing at all to prevent someone from actually building a school out of fish! It is just not a good idea. Therefore, we dismiss this idea because it sounds silly, and we understand only what sounds reasonable to us.
These examples are not limited to English. All natural languages have similar properties. This ambiguity in natural languages matches the efficient thought process that we have, but unfortunately, it also matches the inaccurate thought process, too. Since we communicate our thoughts in words, it becomes challenging to express concepts with precision; it requires conscious effort to do so, bot on the part of the source of the communication, and on the part of the recipient. If we start thinking loosely about different concepts, we may end up mixing them together erroneously, just as what we would be doing if we mix apples and oranges and count them all together as being one entity. The identity law emphasizes the importance of defining concepts precisely.
Defining concepts clearly and precisely is key to proper thinking.
So, what?!
equivocation.
The law of identity is about concepts, not words or physical objects. No two concepts are the same. The tiniest differences between concepts can make a big difference in conclusions built on them. Sometimes the differences are irrelevant and have no effect on the conclusion, but this cannot be stated with confidence until such differences have been shown to have no effect on the conclusion. Using a word or a concept loosely in an argument when it has two different meanings within the same argument is a logical fallacy known as equivocation. An example is the argument: ‘Bats are nocturnal animals; I have a baseball bat; therefore, I have a nocturnal animal.’ Equivocation in the previous example is very obvious, but it is not always as obvious as this. The word ‘bat’ in the first premise has a totally different meaning than in the second premise. What matters is the meaning, not the word. ‘Bat’ the animal is not equivalent to ‘bat’ the baseball bat. Try to think of other examples of equivocation.
In mathematics
Ambiguity is unacceptable in mathematics. Everything in mathematics must have only one meaning in its context. Of course, in different contexts of mathematics, symbols can have different meanings, but explicitly stating the meaning is always advised and preferred. Clarity and precision is a good rule to apply to the thought process in general. Although it goes against the ‘instinct’ of being efficient, it brought humanity a long way from the stage of the hunter-gatherer till the present.
Consider the following problem:
If \(i^2=-4\), what is the value of \(i\)?
The value of \(\sqrt{-4}\) is \(2i\) where \(i\) is the imaginary unit of complex numbers; i.e. \(i^2=-1\). It is tempting to write \(i=2i\), which implies that \(1=2\). This is wrong, of course. The reason it is wrong is because \(i\) in the head of the question is not the same as \(i\) the imaginary unit. The former \(i=-4\) is not the same as the latter \(i=-1\). Canceling them out is wrong! In mathematics, it is assumed that the same symbol has the same meaning all through its context. Therefore, we avoid using the symbol \(i\) for anything other than the imaginary unit in contexts where there are complex numbers. The same applies to common mathematical symbols like \(\pi\) and \(e\).
Second: Law of non-contradiction
not (A and not A)
Nothing can both be (itself) and not be (itself)!
This law of thought might not be as obvious or intuitive as the previous one. The most childish example of how this law might not apply is when someone says “I feel somewhat hungry.” So, are they hungry, or not hungry? They are not really hungry, but they are not really not hungry either. So, can someone be hungry and not hungry at the same time?! That's why we have to go back to the first law: that of ‘identity.’ The expression ‘somewhat hungry’ is not the same as the expression ‘hungry’ or the the expression ‘not hungry.’ Thinking of the three expressions as one and the same concept is wrong. If we do that, we consider that ‘hungry’ = ‘somewhat hungry’ when they are not equal! ‘Hungry’ = ‘hungry’ only! So, how does the second law of thought apply to this situation? It applies, because one cannot be both ‘somewhat hungry’ and ‘not somewhat hungry.’.
The minimum number of distinct things
Ask yourself this: ‘What is the minimum number of distinct things that must exist to explain the diversity in the universe?’ By the word ‘distinct’ I mean things that are not the same. Obviously, if nothing existed, there would be no diversity whatsoever and, in fact, nothing would exist! If only one thing (entity or state) existed, can this produce diversity? If I give you a single brick and ask you to build something out of it without altering it in any way, would you be able to build anything at all from this brick other than the brick itself?! Only one brick in only one state can never produce any diversity. But if I allow you to change the ‘state’ of the brick; e.g. by cutting it into smaller pieces, then you'd be able to make something out of the brick other than the brick. Or if I give you several bricks, you'd still be able to make something from them other than a single brick, even without changing the ‘state’ in which they are. Therefore, at least two distinct entities or states must exist in order to explain your own existence. Why?
You exist at this moment, thinking about different distinct ideas. This would not have been possible if not for the existence of at least two distinct entities or states. If the words you are reading are also not the words you are reading, then there is a single entity that is whatever you are reading. And if you are reading that entity and also not reading that entity, then the activity of ‘reading’ itself loses its meaning and becomes void. And if you are doing a certain activity and also not doing that certain activity, then the concept of ‘doing’ becomes meaningless and void, too. And if you do exist and also do not exist, then your very existence is meaningless and void, and so is the existence of every single concept you are thinking of. But this is not true, because you are thinking of several distinct concepts now! Therefore, nothing can be and also not be, because this will reduce everything to a single entity, which is incompatible with our very existence.

not ‘A’ (red) but not both
In this sense, the meaning of ‘not A’ as mentioned above is not that only two atomic things exist, namely ‘A’ and ‘not A.’ It means that ‘not A’ is everything that is distinct from ‘A.’ The word ‘atomic’ means something that cannot be simplified further or broken down further. There can be a million distinct entities or states; one of them is ‘A.’ The expression ‘not A’ means the other 999,999 entities or states that are distinct from ‘A.’ Any of those entities or states is ‘not A.’ The expression ‘not A,’ therefore, does not refer to an atomic entity or state, but to a group of entities or states that are distinct from ‘A.’. If the law of non-contradiction did not hold, then ‘A’ would not be distinct from the 999,999 entities or states; therefore, only 999,999 entities or states would exist, not a million! Repeating this for each of the 999,999 entities or states, if the law of non-contradiction did not hold, they would be reduced eventually to only one entity or state.
The law of non-contradiction is about the presence of two or more distinct entities or states.
Reality versus the truth
A thing cannot both exist and not exist. Someone who may have some background in physics may argue that uncertainty is built in the universe itself. Therefore, how can we be certain that something cannot both exist and not exist? There is a very important distinction to be made here between ‘reality’ and ‘the truth.’ Failing to make this distinction violates the law of identity, and leaves us prone to becoming confused and making mistakes. The following discussion is about what I believe the words ‘reality’ and ‘the truth’ refer to, but you can call them whatever you want, as long as the meaning of the concept is clear and does not change within the same context.
Imagine that you are presented with a closed box that you are not allowed to touch or examine in any way. If you are asked whether the box is empty or not empty, what would your answer be? You may say something like “I cannot know,” or “It may be empty or not empty.” However, the reality is that the box is either empty or not empty, but not both together. Now, if you are allowed to hold the box in your hands and perhaps shake it to get more information about its contents, but you are not allowed to open it, then you will start to form some ideas about the contents, both qualitatively and quantitatively. What if you hold it up and find that it is quite light?! What if you shake it and find that no sound or perceptible difference is produced when you do so?! You may conclude that the box is empty, which is quite reasonable. But what if the box is completely filled with a light block of polystyrene foam or sulfur hexafluoride, a gas much heavier than air? The box would not be empty, then! Your knowledge of what is in the box is not the same as what really is in the box. If you are allowed to open the box and examine the contents, you may be able to get more information and change your idea about what is in the box. But if the box has sulfur hexafluoride in it, you may miss it completely, because it is colorless and odorless! In more sophisticated philosophical arguments, it can be argued that nothing can give you certainty about what is really in the box!
Uncertainty is related to our ‘knowledge,’ not to what things ‘really are.’

do not move. However, you will see them as if they moved.
Looking at an angle will abolish the illusion.
It does not matter what you know or you think you know about the contents of the closed box. As long as the box remains closed, the contents are what the contents are, and they are not what they are not. If it contains only air, then it cannot not contain air. If it contains a solid block of wood, then it cannot not contain a solid block of wood. If it does not contain toys, then it cannot also contain toys. The truth is absolute and immutable. By ‘absolute’ I mean that the truth is existent regardless of anything else, even our own existence. If it is true that the universe had existed before mankind did, then this is the absolute truth, even if mankind was not there to realize this truth. All mathematical theories existed before we knew them, but we simply had not known them yet. There was no time at which the logarithm of 1 was not zero, even before we knew the concept of a logarithm! By ‘immutable’ I mean that the truth does not change. The truth has been and will always be the truth, and what is not true has been and always will be so. The truth is singular. There is no distinct versions of the truth. There is only one non-atomic truth, as we will discuss later.
Reality is a different matter. ‘Our reality’ is merely a consensus on what we think to be true. Reality is ours, and I would not describe it as the reality. What is real depends on our existence and knowledge. Reality changes according to our knowledge. In ancient times, what we consider to be imaginary creatures like the Pegasus and unicorns were considered very real! Some of us until the present day consider the evil eye an indisputable reality, while others consider it superstition. Not only that! In the field of science, the presence of the luminiferous aether was considered a reality until the late nineteenth century. Diseases like cholera and the plague (also called ‘black death’) were believed to be caused by miasma, which is air pollution, and so was malaria, the name of which literally means ‘bad air.’ Until relatively recently, the smallest subatomic particles were considered to be electrons, protons, and neutrons. At present, both protons and neutrons are believed to be formed of three quarks each. At every stage in history, reality was different depending on knowledge and common belief.
Uncertainty is related to ‘our reality,’ not to ‘the truth.’

with color blindness.
Therefore, I make a clear distinction between the truth, the existence of which is absolute and immutable, and our reality, which depends greatly on our knowledge and is limited by our ability to observe. All what we know about the physical world came through observation. Observation is, in turn, dependent on our senses and our technologies, but the ultimate portal of information to our minds is through the senses. Whatever is beyond our senses is completely known to us. This does not change the fact that it may very well be true. It does not prove that it is true, but it cannot deny it either. We simply do not know! And this is the source of our uncertainty.
Our reality varies even from one individual to another. Consider someone who suffers from color blindness. To the right is a photograph that shows the simulated vision (at the bottom) of such patient. To them, a green apple and a red apple look almost the same; i.e. in their reality, their ‘red’ is equivalent to their ‘green.’ Their reality does not change the fact that the two colors represent distinct wavelengths of light (to the best of our knowledge.)
The law of non-contradiction speaks about the truth, not about our reality. In the realm of thought, nothing can both be and not be. But many things can be unknown to us; i.e. we have no idea if they are or if they are not. However, from what we discussed before, we know that things cannot both be and not be. What things are is analogous to the contents of the closed box given in the example above. What we know about the contents varies and changes, but it does not change the contents themselves.
Dialetheism... what?!
It was suggested by some that something can be true, and its negation can be true, too. This was called dialetheism, which derives from the Greek word διαλεθεια, meaning ‘non-duality.’ Non-dualism as a philosophy is most evident in some Far East religions, as opposed to dualism, which is most evident in Western philosophy and religions. But the core concepts behind these are not the same as the law of non-contradiction. Dualism suggests that the entire existence is in one of two realms: God and matter, abstract and material, etc... Non-dualism suggests that the realms of existence are not just two; that more realms of existence are there. The law of non-contradiction is not about describing or enumerating the realms of existence. It is about stating that there is at least two distinct entities or states in existence. So, based on this understanding, God cannot exist and not exist at the same time. If He exists, then He must be distinct from other things that exist. There is nothing about the law of non-contradiction that puts a ceiling on the number of realms in existence, or the number of entities or states that can exist in any of those realms.
Dialetheism is often used to explain sentence such as “I am certain about the things I am uncertain about.” The sentence seems to suggest that I am both certain and not certain at the same time. If we accept this meaning, then the law of non-contradiction does not hold. But let us examine such sentence more closely. Let the things that I am not certain about be \(U\). Therefore, the phrase ‘the things I am uncertain about’ can be replaced by \(U\). The original sentence, thus, becomes “I am certain about \(U\).” So, am I certain about \(U\) or uncertain about \(U\)? I refer the reader back to the law of identity. What does the word ‘certain” mean in the two sentences? By ‘the things I am not certain about,’ I actually mean ‘the things I have knowledge about not enough to form an opinion about them.’ By ‘I am certain about \(U\),’ I actually mean ‘I have enough information to enumerate all things \(U\).’ So, the word ‘certain’ does not mean the same thing in the two phrases. The original sentence can easily be rephrased as “I have enough knowledge to enumerate all the things that I know about not enough to form an opinion about them.’ The apparent paradox has vanished!
Acceptance of dialetheism leads to acceptance of the principle of explosion, by which anything can be proven. Consider the following example: ‘If I have one apple, then I have two apples.’ The statement ‘I have two apples’ falls most certainly within the scope of the statement ‘I do not have one apple,’ since the latter means any number other than one. If I am to accept that ‘I do not have one apple’ is true as well as ‘I have one apple,&rsquop, then the conditional statement ‘If I have one apple, then I have two apples’ becomes true and acceptable. If this is the case, I will give you one of the two apples I have and, remaining with one apple again, I will have two apples, etc... Complete nonsense! Isn't it?! The reader is encouraged to think of other examples of the principle of explosion. Let your imagination go wherever it wants. There is no limit!

Another example in which dialetheism is often referred to is the famous liar's paradox. Stating it simply, if someone says to you “I am not telling you the truth,” are they telling the truth or not? If they are indeed telling you the truth, then they are not telling you the truth, just as they said! And if they are not telling you the truth, then their statement is a lie, and they are indeed telling you the truth! So, can they be both telling you the truth and not telling you the truth? If so, that would be a clear violation of the law of non-contradiction.
The semantic theory of truth, based on the works of Kurt Gödel and Alfred Tarski, tells us that meaning is what matters when we are considering truth or falsity, not just words. Any language does not intrinsically have the tools to express the truth or falsity of all statements made in that language. We need a metalanguage (i.e. a language about the language) to express the truth or falsity of statements made in that language. Therefore, any natural language is not, in and of itself, capable of expressing the truth or falsity of its own statements without the possibility of ambiguity. This is most evident in the liar's paradox. Trying to both state something and express the truth or falsity of that statement at the same time leads to ambiguity. When someone says “I am not telling the truth,” do they mean ‘the truth about the sentence they are saying’ or ‘the truth about something other than the sentence they are saying?’ If they mean to inform about the sentence they are saying, then ambiguity results because of the inherent limitations of the language itself. This is related to Gödel's incompleteness theorems. There are things that are simply not doable! And if they mean to inform about something other than the sentence they are saying, then the paradox disappears, because the meaning is what matters. There is absolutely no need for such thing as dialetheism to explain the liar's paradox.
Meaning is the most important when considering the laws of thought, since they are concerned with concepts rather than anything else.
In mathematics
Sometimes we prove something in mathematics by showing contradiction. One famous example of this is a proof of why the square root of 2 is not a rational number. Suppose that the square root of 2 is a rational number in the form \(a/b\) where both \(a\) and \(b\) are integers, and that \(a/b\) is irreducible, meaning that there are no common factors that divide both \(a\) and \(b\). Take a note of that! If there are any common factors, we can cancel them out by division and reach an irreducible form of the fraction. Therefore, \(a/b=\sqrt{2}\), which means that \(a^2=2b^2\). This necessitates that \(a^2\) is an even number, since it is the product of 2 and another integer. No odd number can be squared to give an even number. Therefore, \(a\) is itself an even number. Hence, it can be represented as the product of 2 and some other integer \(k\). If we substitute \(a=2k\) in the original equation, we get \(4k^2=2b^2\), which is reduced to \(2k^2=b^2\). In a similar way of reasoning to what we concluded about \(a\), we can conclude that \(b\) is an even number, too. If both \(a\) and \(b\) are even numbers, then they are both divisible by 2. Compare this to the note we took before. Since \(a\) and \(b\) cannot both ‘have 2 as a common factor’ and ‘not have any common factors,’ there exists no such rational number \(a/b=\sqrt{2}\).
Similar reasoning can be found often in mathematics. Sometimes it is even the only way of proving something, or at least the only known way.
Consider the following problem.
If \(a\) is divisible by 210, and \(14a\) is not divisible by 3, what are the possible values of \(a\)?
We use the notation \(b \mid a\) to indicate that \(b\) divides \(a\), or that \(a\) is divisible by \(b\). If \(210 \mid a\) and \(3 \mid 210\), then it follows that \(3 \mid a\). If \(3 \nmid 14a\), then \(3 \nmid 14\), which is true, and \(3 \nmid a\). There can be no number such that \(3 \mid a\) and \(3 \nmid a\). Therefore, there is no value of \(a\) that satisfies the previous conditions.
Failing to think about the law of non-contradictions in problems like this one may make them seem exceedingly difficult, or even unsolvable.
Third: Law of the excluded middle
Either A or not A
Either something is, or it is not. There is no ‘middle’ alternative!
Does this sound too ‘black and white’ to be accepted?! Does everything in existence really fall into one of two categories? Can everything in existence be reduced to this kind of dichotomy? Again, it depends on the meaning you understand. We made it clear in our discussion about the law of non-contradiction that no ceiling is imposed on the number of distinct entities or states that can exist. The law of the excluded middle seems to put such ceiling at the number 2. Right?! No!
The law of the excluded middle puts everything that is not ‘A’ into the category called ‘not A.’ If a million distinct entities or states exist, then ‘A’ is one of them that is distinct from the remaining 999,999 ‘not A’ entities or states. If the reader remembers, a discussion about the non-atomic nature of the truth was promised. Here it comes!
The non-atomic truth
The truth is not a simple thing that can be considered indivisible. The truth should be considered as the amalgamation of many smaller atomic entities, each of them is necessarily true, and the negation of each of them is necessarily false. Pieces of the truth fit together as pieces of a puzzle do. They complete each other in a coherent way. This means that no piece of the truth contradicts another piece. One of the sources of confusion is that we do not have all the pieces of the puzzle; i.e. we do not know all the truth.
Let us go back to the example of the closed box. Imagine that the box contains 4 envelopes and 3 paper clips. It is, therefore, false that the box does not contain 4 envelopes and 3 paper clips. How about the statement ‘the box contains 4 envelopes?’ Isn't that statement true?! How about the statement ‘the box contains 3 paper clips’ or ‘the box contains 3 envelopes and a paper clip?’ Are those statements not true, too?! How come, then, that there is no middle alternative?!
Here is the trick: the law of the excluded middle speaks about a certain defined component of the truth, or about all the truth, but most certainly not about a loose definition of what the truth can be. If you are asked about the entire contents of the box and your answer is that it contains 4 envelopes, your answer is indeed wrong! If you are asked about one of the contents of the box and your answer is that it contains a paper clip, your answer is right! All the truth in this situation is the entire contents of the box. Partial truth in this situation is that the box contains at least 1 and at most 4 envelopes, and/or at least 1 and at most 3 paper clips. Any combination of that will still be partial truth, so if you answer that it contains 2 envelopes and 3 paper clips, that will qualify as a right answer, too. So, what is the partial truth in this case exactly? It is quite long, so brace yourself.
The box contains 1 envelope, 2 envelopes, 3 envelopes, 4 envelopes, 1 envelope and 1 paper clip, 1 envelope and 2 paper clips, 1 envelope and 3 paper clips, 2 envelopes and 1 paper clip, 2 envelopes and 2 paper clips, 2 envelopes and 3 papers clips, 3 envelopes and 1 paper clip, 3 envelopes and 2 paper clips, 3 envelopes and 3 paper clips, 4 envelopes and 1 paper clip, 4 envelopes and 2 paper clips, 4 envelopes and 3 paper clips, 1 paper clip, 2 paper clips, or 3 paper clips.

Either any of the previous is true, or none (i.e. not any) of the previous is true. There is no middle ground. This illustrates how the truth can be very overwhelmingly complex. Talking about a box with 7 objects in it resulted in 19 different possibilities of partial truth. Things around us seem to have much more than 7 objects, and to interact with each other in much more than 7 ways. That's why the truth is complex beyond comprehension; probably infinitely complex, too.
The truth is non-atomic; it is rather exceedingly complex.
The apparent presence of a middle ground that violates the law of the excluded middle results from the lack of precision in our definitions. Therefore, when people go under oath in courts, they swear to ‘tell the truth, all the truth, and nothing but the truth.’ Partial truth is still true, but we need to know all the truth.
Going back to our box, if you understand that the sentence ‘the box has 2 envelopes’ means that the box has only 2 envelopes, then the sentence would be false, because you are then looking for all the truth, not partial truth. But for partial truth, the sentence has to be understood as ‘you can find 2 envelopes in the box;’ in which case you can either find 2 envelopes in the box, or you cannot find 2 envelopes in the box, with no middle ground! The sentence is not understood to limit all what you can find in the box to 2 envelopes, but to include the 2 envelopes in whatever you can find in the box. If the box has 2 envelopes or more (with no limit), or if it had 2 envelopes and the entire universe but not other envelopes, the statement would still be true, and its negation would be false. If the box had 1 envelope, though, the statement would be false, and its negation would be true: ‘you cannot find 2 envelopes in the box.’ Everything goes back to meaning. Everything is tied to the law of identity. Thinking of distinct concepts as being one and the same leads to confusion and errors.
Exclusive or
When we say that something either is or it is not, we mean what in logic is known as the ‘exclusive or,’ or exclusive disjunction. This necessitates that a thing cannot both be and not be, in compliance with the law of non-contradiction. If it is true that something is, it is necessarily false that it is not; and if it is true that something is not, it is necessarily false that it is. The use of the word ‘or’ in natural language is ambiguous. If you ask your parent or spouse for something to eat, and they tell you you can eat eggs, cheese, jam, or sausages; they are probably not telling you to choose only one of those. They are giving you options, and you may choose all of these options if you want. You may end up eating eggs, cheese, jam, and sausages. On the other hand, if you are asking someone about how to go to a certain address, and they tell you that you can take the bus or the train, they actually mean that you have to choose between taking either the bus or the train, but not both. This latter meaning of the word ‘or’ is what is equivalent to the ‘exclusive or,’ and it is what is meant in the law of the excluded middle.
Dichotomy in our daily life
The law of the excluded middle and the dichotomy it implies is useful in our daily life. Suppose you are selecting from a group of candidates for a certain position. If the number of candidates you are selecting from is relatively small, the task might not be that difficult. But if the number is large, it will be difficult to consider them all together. Most people would go through the resumes, filtering out one by one those who are not suitable for the position. Doing so, they classify the candidates into either suitable or not suitable for the position, with no third option. When the numbers are reduced, they can now concentrate on those who were classified as suitable, and totally ignore those who were classified as unsuitable. Again, they can repeat this dichotomous process to classify suitable candidates into impressive and not impressive, with no third option. They can then limit their selection process to those who were deemed impressive.
This process of dichotomous selection is very common. Someone who is looking for job opportunities in the newspaper will scan the jobs, marking only those which they think to be appealing. When they are finished with scanning, they limit their comparisons and attempts to those jobs that were deemed as appealing. Granted, if they fail to get any of those jobs, they may modify the characteristics on which they classified jobs as being appealing, but now the definition of appealing has changed, and the new dichotomous selection process cannot be compared to the old one, because the meanings are not the same.
The least number of choices, for anyone to have real choices, is two. This simplifies things greatly. Even if this means to reduce the number of choices by separating them into two groups of different priorities or preferences, this still goes a long way in facilitating selections. This, again, illustrates the minimum number of distinct entities or states needed for diversity; something that was discussed above. By selecting from the minimum, we make it easier on ourselves.
Often, logical conclusions are reached using this law of thought. For instance, if someone was locked in a room with only two doors, and you were standing guard on one of them and did not see anyone coming out. If you entered the room and found that that person is not there, you'd conclude that they went out through the other door, since they did not go out through the door you were guarding, and there was no third alternative. This kind of argumentation is called ‘reductio ad absurdum,’ or ‘argumentum ad absurdum,’ which is Latin for ‘reduction to absurdity.’ In our previous example, it is absurd that the locked person would have gotten out through the door you were guarding without you knowing it; therefore, they must have gone out through the other door (or doors, if the room had more than two.) Essentially, you'd think of that situation as ‘the person either have gotten out through the door I was guarding, or through the other door, with no alternative options; they did not go through the door I was guarding; therefore, they must have gone out through the other door.’ This is a very common use of the law of the excluded middle.
Sorites paradox

to be a heap if we take
a grain of sand from it?
The name of the sorites paradox is derived from the Greek word σωρητες, meaning ‘heap.’ The paradox simply asks the following question: “Does a heap of sand cease to be a heap of sand if we take away a grain of sand from it?” The obvious answer to this question is that it doesn't! But if a heap of sand contains a million grains of sand, and taking away a single grain does not make it cease to be a heap, then a heap of 999,999 grains of sand is also a heap. Taking another grain of sand from that heap does not make it cease to be a heap; hence a heap of 999,998 grains of sand is also a heap of sand. We can continue this until we conclude from it that a single grain of sand is a heap of sand, and if we take away a single grain of sand from it, then no grains of sand is also a heap of sand!
Thinking about this paradox for a little while makes one believe that there must be something other than ‘a heap of sand’ and ‘not a heap of sand.’ In other words, there has to be some other option; hence the law of the excluded middle is void! But is it?!
The first law states that an entity is itself. The ambiguity of the natural language goes against that law. A heap of a million grains of sand is not a heap of a thousand grains of sand. Taking a grain from a certain heap of sand may still leave it within the range of what is considered a ‘heap,’ but taking a grain from another heap of sand may not have the same effect. The problem here is caused by the ambiguity of natural languages. The laws of thought require precision; natural languages are not precise. There are many words in natural languages that intentionally vague, and this makes them efficient, because we can express a very rough approximation with those languages. Examples are ‘bunch,’ ‘handful,’ ‘stack,’ ‘a bit,’ ‘much,’ etc... Solving that paradox does not invalidate the law of the excluded middle, but rather tries to work around the vagueness of such natural language expressions.
In mathematics
Mathematics is such an ideal world. In the realm of abstract concepts, we have no doubts. We may still not know things, but when we know them, we have no doubts about them. The law of the excluded middle speaks of things that we know, not of things that we do not know. The unknown is certain to us in only one way: that we do not know it! Again, the third law states that we can either know something, or not know that thing; there's nothing in between. There are indeed certain things in mathematics that are unknown to us, and there are even certain things that have been proven unknowable. For those things, we know for certain that we will not know them! As paradoxical as that might sound, it illustrates the fundamental difference between knowledge of the truth and existence of the truth. They are not the same, and will never be the same.
Many times in mathematics, we find ourselves reaching a conclusion by considering two opposing situations: either this situation or not this situation. For example, either \(a\) equals zero or \(a\) does not equal zero. There is room for confusion here, if we do not observe the first law and realize that truth is non-atomic. The meaning of ‘not equal to zero’ is not the same as the meaning of ‘equal to one.’ The former expression involves infinitely many more numbers than the number one.
Another example that I came to like is the answer to the question: ‘Is 2 greater than or equal to 2?’ If the answer is ‘yes,’ does this mean that 2 is greater than 2? If the answer is ‘no,’ does this mean that 2 is less than 2? Think carefully!
We know that \(2 \lt 2\) is a false statement; therefore \(2 \nless 2\) must be a true statement. There are no other alternatives. But the statement \(2 \nless 2\) is non-atomic; it is equivalent to \(2 \ge 2\), which can be simplified to \(2 \gt 2\) or \(2 = 2\), since the identifiable outcome of comparing two entities is exclusively one of the three states ‘greater than,’ ‘equal to,’ or ‘less than.’ If any of the statements \(2 \gt 2\) or \(2 = 2\) is true, it is enough to make the statement \(2 \ge 2\) true. But the statement \(2 \ge 2\) does not mean that \(2 = 2\) and \(2 \gt 2\); it is simply the equivalent of \(2 \nless 2\).
Some mathematicians would object to the use of the law of non-contradiction and the law of the excluded middle; e.g. intuitionists. Also, some fields of mathematics seem not to validate these two laws; e.g. many-valued logic. Again, it all depends on how you understand the meaning. An intuitionist is a constructive mathematician, who will require constructing any mathematical entity before accepting its existence. In this regard, they tend to object to the law of the excluded middle, since proving that something does not exist is not the same as proving that the contrary exists in their opinion. Constructing a mathematical entity means to prove its existence in an algorithmic way, or to provide an example for its existence. The problem with this is that one must construct from simpler entities or try to find an example of a certain entity in an infinite number of entities. There has to be a stage at which no simpler entities exist; i.e. we cannot proceed infinitesimally trying to construct mathematics. We cannot search infinite mathematical entities in search for an example, either. Therefore, something has to be accepted without constructing it from simpler entities or providing an example. Furthermore, we stated above that the laws of non-contradiction and the excluded middle do not impose a ceiling on how many distinct entities can exist; they simply classify things into two distinct, non-overlapping groups. Therefore, if something cannot exist in one group, but it can exist, it must exist in the other group. As for the many-valued logic, the same applies. The meaning of ‘not true’ does not become ‘false,’ but ‘false or indeterminate.’ The example of \(2 \ge 2\) is similar to this.
An example of the use of the law of the excluded middle in mathematical proof is to prove that there exists a number \(a^b\) such that both \(a\) and \(b\) are irrational, but \(a^b\) is rational.
Consider the number \(\sqrt{2}^\sqrt{2}\). It has been proven above that \(\sqrt{2}\) is irrational. Therefore, if the number \(\sqrt{2}^\sqrt{2}\) is rational, we have our proof. If the number \(\sqrt{2}^\sqrt{2}\) is irrational, then consider the number \(\left(\sqrt{2}^\sqrt{2}\right)^\sqrt{2}=(\sqrt{2})^{(\sqrt{2} \times \sqrt{2})}=(\sqrt{2})^2=2\), which is rational. Therefore, there must exist two irrational numbers \(a\) and \(b\) such that \(a^b\) is a rational number.
An intuitionist would not accept this proof, because it assumes that \(\sqrt{2}^\sqrt{2}\) is either rational or irrational with any middle possibility excluded, but it does not show constructively that \(\sqrt{2}^\sqrt{2}\) is irrational indeed. However, the definition of ‘irrational’ is not ‘real,’ ‘transcendental,’ ‘algebraic,’ or anything of this sort. It simply means not rational. It can be anything that is not a rational number.
Fourth: Indiscernibility of the identicals and identity of the indiscernibles
These laws of thought are relatively new additions to the classical three laws, and are usually attributed to Leibniz. In a nutshell, the law of indiscernibility of the identicals states that if two entities or states are indeed one and the same thing, no discernible differences exist between them at all. Discernible differences are such differences that can ever be known. Indiscernibility means that no konwable differences can ever exist between the two entities. This law is mostly undisputed. There is, therefore, an important distinction to make: that between discernible differences and known differences. The latter are included within the former.
| A and B are identical | A and B are not identical | |
|---|---|---|
| Discernible differences | do not exist | exist |
| Known differences | cannot exist | Perhaps? |
The dichotomy we discussed earlier comes to the rescue here. Two entities ‘A’ and ‘B’ are either one and the same (i.e. identical,) or not one and the same. This is represented by the header row in the table above. Discernible differences can either exist or not exist. The law of indiscernibility of the identicals necessitates that if ‘A’ and ‘B’ are identical, no discernible differences exist. Therefore, if they are not identical, at least one discernible difference must exist. This is represented by the second row in the table above. What exists is not necessarily restricted to our knowledge, as discussed above. Therefore, whether we know about existing discernible differences is not the same as their existence. If no discernible differences exist, we cannot know anything about them, obviously. But if they do exist, we may or may not know something about them. This is represented by the third row in the table above.
The difference between the law of indiscernibility of the identicals and that of identity of the indiscernibles is essentially where we start our assertion. For the indiscernibility of the identicals, we start by asserting that two entities or states are indeed identical. This is equivalent to the column with the blue heading in the table above. For this column, no discernible differences exist; therefore, no known differences can exist. Pretty simple!
For the identity of the indiscernibles, however, it is quite different. The assertion point here is that we do not know any differences between two entities or states. This is represented by the row with the red heading in the table above. For us to be certain about something in this table, it must either fall in no cell at all (like what happened in the discussion above,) or fall into a single cell. If we do not know any differences, though, this may fall in either the ‘cannot be known’ cell or the ‘perhaps?’ cell! Do we have no known differences just because we do not know the differences (that exist) yet, or because there are no such differences in existence? We will never be able to ascertain this in many situations.
If two entities are one and the same (i.e. identical), no discernible differences exist between them.
Meanings
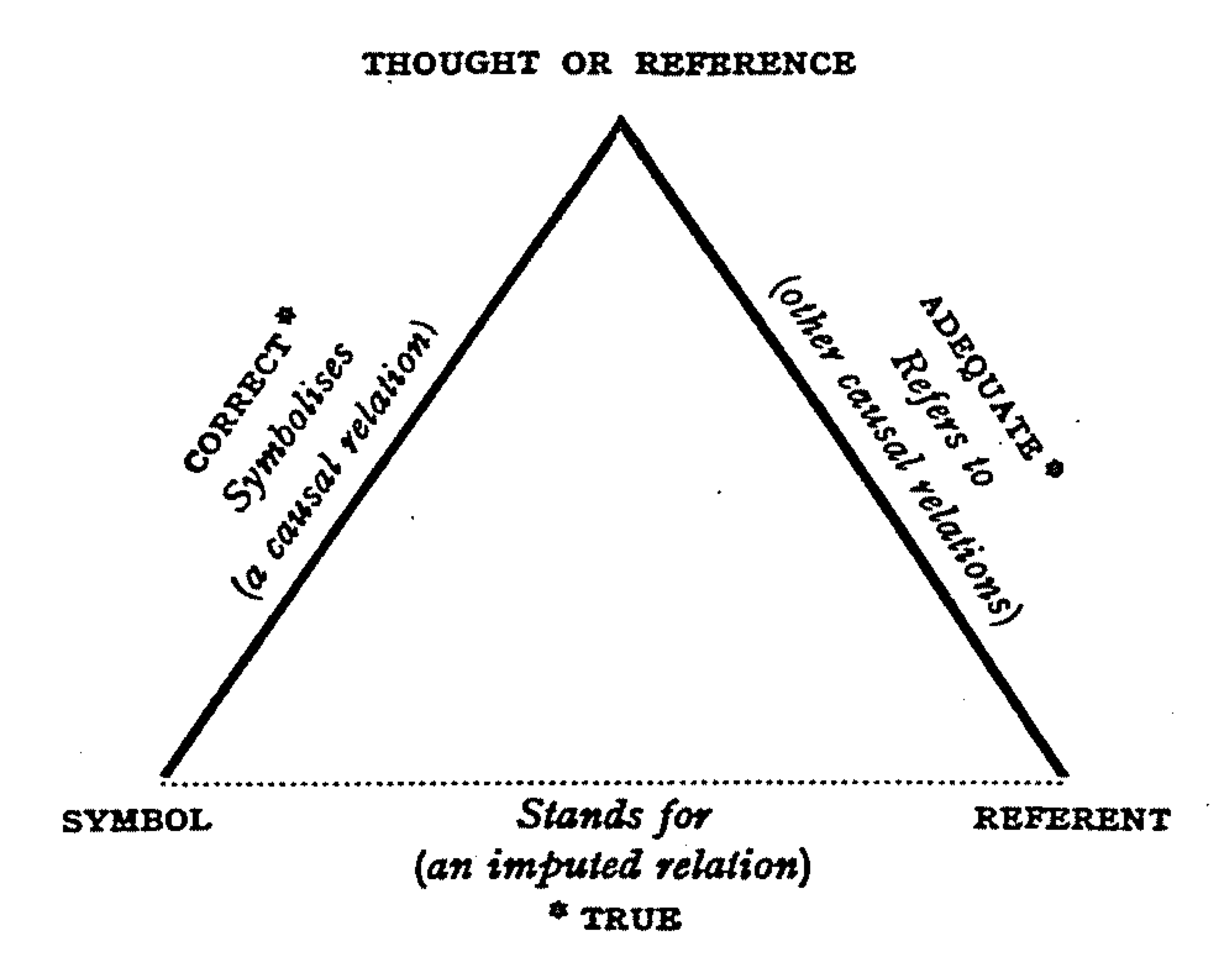
Another distinction becomes important here, and it takes us back to the discussion of concepts versus physical objects. The triangle of reference (although not the only theory in semiotics) describes a relation between the concept held in the mind (also called the reference,) the physical object that it refers to (also called the referent,) and the word or any method of communication of such concept (also called the sign.) For every referent that we know, there is a reference in our minds. We indicated this earlier by discussing that the realm of abstract concepts is wider than, and encompasses that of, the realm of physical entities. For some subjective pieces of knowledge, we may not have a particular sign to describe them, as is the case when one cannot find proper words to describe their feeling. But what is more frequent on a regular basis is the case of the absent referent, in which concepts do not correspond to a physical entity. Consider abstract ideas like justice, freedom, peace, etc... This further emphasizes the concept that concepts are more than physical objects.
But concepts are not always absolute. Concepts (references) exist exclusively in the minds of their holders. A book is not full of references, but rather full of signs that are translated into references in the mind of the reader. You cannot take any references from a book written in a language that you cannot read, because it contains no references, but rather contains signs. Everyone creates their own concepts in their own minds; therefore, they can be completely aware of every aspect of such concepts, but no one else can tell every aspect of someone else's concepts. We can try to communicate our concepts and adjust them as necessary in order to reach a consensus. For instance, the concept of ‘freedom’ in some countries at present is, unfortunately, that one is not incarcerated! It does not extend to some basic human rights such as the right to have and express an opinion. People in various communities have different notions of the concept ‘freedom.’ Only through communication can they remodel their concepts and reach a unified understanding. Concepts are different than physical entities in this way: we can create and reshape our concepts in any way we want, and we can have full knowledge of every aspect of our concepts with no uncertainty about the concept.
But the referents that concepts refer to are outside of our minds. We cannot possibly know everything about the referent. References are limited by what we observe about the referent. No one can claim to really know everything about anyone else, no matter how close they are to them. At the very least, you cannot possibly know what is in their minds! For as long as I lived, I observed that things fall down to the ground. This created the concept of ‘gravity’ in my mind. However, I cannot possibly be 100% certain that gravity existed and will exist at every time and place as it exists now. I cannot claim to know everything about gravity. Is gravity some sort of force as Isaac Newton suggested? Is it a distortion in space-time as Albert Einstein suggested in his General Relativity theory? Or is it caused by gravitons as it has been recently suggested? Each of those theories works, but they all have their weak points. We do not know what gravity really is. We know the meaning of gravity, however. It is something that pulls things towards each other. But I can claim with confidence that I know everything about what I call ‘success,’ for instance, because this is a reference in my mind with no referent in the physical world. I have full control over this concept.
Monadic versus polyadic
A monadic property (from Greek ‘μόνος,’ meaning ‘one’) is a property of an entity itself; related to the essence of the entity, not in relation to anything else. A polyadic property (from Greek ‘πολύς,’ meaning ‘much’) is a property that depends on at least two entities to be defined. When it depends on exactly two entities, it is called a dyadic (from Greek ‘δυο,’ meaning ‘two’) property. The same terminology applies to entities or relations. An abstract entity that can exist and have a meaning on its own is a monadic concept, as opposed to polyadic concepts that are meaningless or incomplete on their own. An example of a polyadic concept is the spatial and chronological relations like ‘before’ and ‘under.’
Only monadic concepts can have exclusively monadic properties. It can be argued that polyadic concepts cannot have only monadic properties, because they necessarily depend on another concept to have a complete meaning; hence, there has to be a certain non-monadic property relating those two concepts. An example is the act of ‘filling.’ One cannot just fill; they must fill something. The meaning of ‘fill’ on its own is incomplete at best, if it is not used in a context that suggests what to fill. The relation between the verb and its object is certainly not a monadic property, because it involves more than one entity. Furthermore, there can be a polyadic property because the verb ‘fill’ can take two objects: that which is to be filled, and that which is used to fill with. A similar concept is that of ‘giving.’ One has to give something. Compare this to the act of walking, talking, eating, or flying. The concept of ‘walking’ is a complete concept of its own. We can give more meaning to it by attaching more concepts, but it is still valid on its own as a complete meaningful concept.
Knowledge is a polyadic property, for one must know something. Furthermore, knowledge is abstract; it is held in the minds of people. Therefore, in many cases, knowledge cannot be considered independently of who knows. What I know is different from what you know. Also, subjective knowledge is very difficult to transfer from one person to another. What I know about the taste of coffee is not the same as what you know about it. The concepts that we hold about physical entities are necessarily polyadic. Our knowledge is not independent of us, of the physical entities themselves, of the process by which we got to know those physical entities, etc... The true identity of a physical entity is a monadic property of that entity. It exists; therefore, it must have certain monadic properties, least of which is ‘existing.’ On the other hand, what we know about concepts in our minds can be entirely accurate and complete, and we can describe them uniquely in terms of monadic properties of those concepts. This does not apply to all concepts, but only to monadic concepets. How does this affect the law of the identity of the indiscernibles?
Identity of the indiscernibles revisited
As discussed above, it is impossible to tell if we do not know any discernible differences between two entities because no such differences exist, or because we simply haven't gotten to know the differences that exist yet. Most things have monadic properties that identify them independently of any other entities. What we know about them, however, is not a monadic property. Consider the following example. The Kuiper belt is disc of small celestial objects, similar to the asteroid belt, that belongs to our solar system. It is approximately 30 times as far away from the sun as Earth is, and it extends about 20 times that distance. Its presence was suggested in the early 20th century, but no direct evidence of its existence was found until the late 20th century. It must have existed prior to its discovery! Therefore, although we had not known anything about it for centuries, it was probably there. Its monadic property of ‘existing’ was there, but the property of ‘humans know that it existed’ was absent.

apprentice» in the famous fictional story
Let us consider a fictional example, but it will illustrate how the law of identity of the indiscernibles can be problematic. Imagine that you could travel back in time with some of our present-day surveillance equipment and install them in the king's palace. You'd then be able to know all the king's secrets from far away, with witnesses confirming your absence from the palace. If you told the king about such secrets, he might come to think that you had spies within the palace. But you could challenge him that you would be able to tell whatever he said when he was certain he was alone. Because of the surveillance equipment, you would be able to do that. The king did not know about the surveillance equipment, but he held the belief that some people had supernatural powers. Because of the lack of knowledge of the king, he would believe that you were identical to a sorcerer, when in fact you were not. In such a situation and similar ones, the law of identity of the indiscernibles fails!
That's why the law of identity of the indiscernibles can only be applied if we know all properties that characterize the entities under consideration, or at the very least all of their monadic properties. In the previous example, for instance, you ‘not being a sorcerer’ is a monadic property of yours, but the king did not know about it. How is it possible to ascertain that we know all monadic properties about something? As we discussed above, this is only possible in the realm of thought, and only with monadic concepts. Anything that has to do with knowledge about any physical entity is necessarily not monadic. Hence, the law of identity of the indiscernibles cannot be used with anything other than abstract concepts that are independent from physical objects.
We do not know what we do not know; therefore, we cannot claim to know everything.
So, if you cannot tell the difference between two monadic concepts in your mind, there is only one of two options: either there exists no difference at all (hence, they are identical concepts), or that the concept is not yours (hence, you are unable to know everything about that concept.) If it was possible for others to put concepts in your mind that are not yours, you would have no way of knowing anything about those concepts other than what they allowed you to know. Therefore, it would be impossible for you to tell the difference between those two concepts. Consequently, you will have to accept that any two indiscernible monadic concepts in your mind are indeed one and the same concept. This is your only option.
Extensional and intensional equivalence
An extension of a concept or a predicate (i.e. description or property) is all things to which that concept applies. For example, apple trees are within the extension of the concept of a plant, dogs are within the extension of the concept of a mammal, chairs are within the extension of the concept of furniture, fear is within the extension of the concept of emotions etc... An intension (notice the difference in spelling from the word ‘intention’) of a concept or an object is a predicate that, together with other intensions, characterize the essence of that concept or object. For example, all the predicates ‘fruit,’ ‘yellow,’ ‘seedless,’ and ‘circular in transverse sections’ are intensions of a ripe banana; and all the predicates ‘has four limbs,’ ‘has fur,’ ‘gives birth to live offspring,’ and ‘sounds like meeoowww’ are intensions of a cat. In view of what we discussed earlier, extensions are a set of referents, while intensions are a set of predicates (references.) The set of all intensions that characterize any concept or object is called the comprehension of that concept or object. Notice that concepts can either be extensions or intensions, but for them to be intesions they have to be expressed in the form of predicates. This means that ‘love’ can only be in an extension, but ‘loving’ can be an intension as well as part of an extension. For example, the extension to ‘the qualities that a good parent has’ includes ‘loving,’ but ‘love’ cannot be a predicate (i.e. description) to anything.
Two entities are said to be extensionally equivalent if their extensions are the same, and intensionally equivalent if their comprehensions are the same. Extensional and intensional definitions are different in that the former lists all elements of the extension of a concept or a predicate, and the latter lists all the predicates of a concept or an object. A definition is meant to characterize something in such a way that there is no room for confusion. Hence, a definition of something is the necessary and sufficient description of that thing to characterize it and distinguish it from other things. Although the previous definition of a ‘definition’ is not perfect, it is the most convincing one to me.
Certain entities are best defined extensionally and others are best defined intensionally. For example, the items produced by a certain factory are best defined extensionally by listing them. Usually, extensions that are small, finite sets are good for extensional definitions, especially when there is no certain easy ‘rule’ to define the concept otherwise. For example, the items produced by a factory are much more easily listed than described by a certain rule. On the other hand, some other things are best defined intensionally. For example, numbers that are divisible by 10 are those that have 0 in the ‘ones’ place. It is impossible to list all numbers that are divisible by 10. But is there a fundamental difference between intensional and extensional definitions? Yes, indeed, there is.
The law of identity of the indiscernibles is applicable for any two entities if and only if those two entities are intensionally equivalent.
Extensional equivalence, where the extensional definitions of two entities are the same, does not necessarily represent identity. If two factories have the same extensional definition; i.e. they produce the same items, they are not necessarily one and the same factory. They just produce similar items. On the other hand, intensional equivalence, where all fundamental predicates of two entities are the same, necessarily indicates identity. Remember that intensional equivalence is when the comprehensions of two entities are the same, which is all their predicates. If we can list all the predicates of two things, and we find them the same, then the two things are identical. But this takes us back to our discussion about the limits of knowledge. If all predicates in the comprehensions of two entities are known and identical, then those two entities are necessarily identical. Intensional equivalence is conditional upon the predicates in the comprehensions being known, which is—as discussed earlier—limited to certain concepts.
In everyday life
Indiscernibility of the identicals is simply commonsense. We use it on a daily basis. If you are in ‘a home‘ that is one and the same as ‘your home,’ it follows naturally that you will not be able to detect any differences between ‘that home’ and ‘your home.’ I feel like discussing this further is a waste of time and energy.
The law of identity of the indiscernibles is no less common in daily use than that of indiscernibility of the identicals, although it is not really a rigorous ‘law’ for most of its daily use. People usually ignore the word ‘might’ in the sentence ‘indiscernibility might mean identity’ and consider that indiscernibility necessarily means identity. That's wrong! If indiscernibility is affected by the limits of your knowledge, then it only means that there is a ‘probability’ of identity, and you have to keep in mind that such probability might actually be zero; i.e. things may turn out to be nonidentical. Lack of knowledge does not give you any solid information so that you may get a quantitative estimate of such probability.

legendary character
‘Mystique’
There is a recurring theme in movies that tells of people who assume the identities of others and try to be exactly identical to them, so people wouldn't be able to tell the difference and, therefore, assume they are one and the same person. You can see it in the movie ‘Face Off,’ in the character ‘Mystique’ in all works based on ‘X-Men,’ and in many more works. The general idea is that people tend to assume that two different entities are the same just because they cannot tell the difference between them. But what else can we do?! If there is no discernible difference between two things, does it seem ‘reasonable’ to assume that they are not the same?! Because if this is the case, we should always be in doubt about everything and everyone we know or encounter every day. This surely does not seem to sound ‘reasonable.’
The fundamental difference here is the distinction between what is likely and unlikely, between what is possible and impossible, but not between what is reasonable and unreasonable. It is totally reasonable (i.e. concluded by proper reasoning) that two indiscernible entities might not be one and the same. But this rarely happens in our everyday life; at least to the best of our knowledge. Furthermore, there is no possible way to ascertain that discernible differences do not exist between any given two entities, since this requires the assertion that everything about those two entities is knowable. Our best is to accept that the absence of observable differences between two entities means they are one and the same. This applies to what we know about physical entities, not concepts, as discussed before. So, we are doing ‘our best’ considering indiscernible physical entities identical, but it is not unreasonable to consider them nonidentical, as unlikely as it may seem to us. Our best is not the absolute truth; considering it to be so is a major defect in the thought process.
We use the law of identity of the indiscernibles in everyday life in a wrong way, but this is our best, which may happen to be completely wrong.
In our natural language, there are certain contexts in which terms and their extensions can be used interchangeably, and others in which they cannot. Consider the term ‘A Swedish man,’ which extends to include the famous Alfred Nobel. In a sentence like “Alfred Nobel instituted the Nobel prizes,” it is perfectly acceptable to use the term ‘A Swedish man’ interchangeably with the term ‘Alfred Nobel’ and rewrite the sentence as “A Swedish man instituted the Nobel prizes.” However, in another context like “A Swedish man founded the Ericsson telecommunications company,” we cannot use the term ‘Alfred Nobel’ interchangeably with ‘A Swedish man.’ It was Lars Magnus Ericsson, also a Swedish man, who founded that company. Now consider the term ‘English people,’ which extends the term ‘English-speaking people.’ The two sentences “I saw some English people this morning” and “I saw some English-speaking people this morning” are not the same. While the latter may replace the former without affecting the truth of the sentence, the former cannot do the same with the latter. In the former example, we used part of the extension (Alfred Nobel) to substitute for the whole extension (Swedish men.) In the latter example, we used the whole extension (English-speaking men) to substitute for part of it (English men.) Contexts in which we can replace a certain term with part of the extension or the whole extension are called extensional contexts. Contexts in which we cannot replace terms with part of or the whole extension are called intensional contexts. Consider the sentence ‘The nuclear codes of the US are under the control of the US president.” At the time of writing of this article, the US president is Barrack Obama, but this will change soon, and that was not true 10 years ago. So, even if the term ‘Barrack Obama’ extends the term ‘US president,’ and so do the terms ‘George W. Bush’ and ‘Bill Clinton,’ none of them can replace the term ‘US president’ in the previous sentence without altering its truth. Thus, that sentence is an example of an intensional context.
Therefore, not all extensionally equivalent terms can be used interchangeably in any context, although they are indiscernible as far as their extensional definitions go. We have to also notice that intensional definitions of entities may change. While the predicate ‘president of the US’ is true for Barrack Obama now, it will change in the future to ‘former president of the US.’ Definitions have to be periodically revised as necessary, and the law of identity of the indiscernibles is affected by changes in definitions. The law applies to the here-and-now definitions, not in an absolute sense.
In mathematics
The ‘equal sign’ in mathematics does not always mean that what is on its right is identical to what is on its left in every aspect. In most cases, we use the \(=\) sign to indicate equivalence in value, but not necessarily in meaning. If two things are exactly identical (i.e. intensionally equivalent), we use the symbol \(\equiv\) to indicate that in mathematics.
Consider the following algorithmic operations:
- Choose a number, square it, then subtract its double from it, and finally add one to the result.
- Choose a number, subtract 1 from it, then square the result.
The previous two algorithmic operations are not the same in meaning or have the same steps, but they are always the same in value. If the first operation is \(f(x)=x^2-2x+1\) and the second operation is \(g(x)=(x-1)^2\), then \(f(x)=g(x)\) in value. The extension of a function is the set of all ordered pairs (or n-tuples) that identify the mapping of the function from its domain to its co-domain (i.e. range.) In any context that is concerned with value only (i.e. the mapping rather than how it is made), \(f(x)\) and \(g(x)\) are indiscernible and identical. However, consider what happens if we want to calculate the expression \(g(x)/h(x)\) where \(h(x)=x-1\).
\[ \frac{g(x)}{h(x)}=\frac{(x-1)^2}{x-1}=x-1 \]The previous calculation is wrong unless you specifically state that it is not defined for \(x=1\). The expression \(g(x)/h(x)\) is extensionally equivalent to the expression \(x-1\) for all values of \(x\) other than \(x=1\). While this can be easily recognized from the non-reduced expression of \(g(x)/h(x)\), it is totally obscure in the expression \(x-1\). Therefore, for all replacements of \(g(x)/h(x)\) with \(x-1\), we must exclude the mapping of \(x=1\) from the extension of the function.
The same applies for the expression \(x\) and the expression \(\sqrt{x^2}\). It is easy to make the mistake of replacing one with another without thinking much. They are indeed indiscernible in many situations, but not all situations. The square root of any number can be either a negative value or a positive value. Therefore, \(\sqrt{5^2}\) is \(\pm5\), not just \(5\). Furthermore, squaring of any negative number eliminates the negative sign. Therefore, \(\sqrt{(-5)^2}\) is also \(\pm5\), not \(-5\). If we want to be correct, we must indicate explicitly that \(x=+\sqrt{x^2}\) for \(x \ge 0\) and \(x=-\sqrt{x^2}\) for \(x \lt 0\).
In certain situations, the meaning of something is essentially the meaning of something else; i.e. they are intensionally equivalent. For example, in our previous discussion about whether \(2 \ge 2\), the meaning of \(x \nless y\) is exactly identical to the meaning of \(x \ge y\); therefore we can state that \(x \nless y \equiv x \ge y\). Also, if we have two sets \(S\) and \(P\), the meaning of \(x \in S \land x \notin P\) is exactly identical to the meaning of \(x \in S/P\) where \(S/P\) is the relative complement of \(P\) with respect to \(S\). We can write \(x \in S \land x \notin P \equiv x \in S/P\).
Traditional vector algebra taught in high schools is another example where the sum of two vectors is extensionally equivalent to the two vectors combined in terms of magnitude and direction, but not intensionally equivalent. For the sum to be intensionally equivalent, we have to assign vectors to points in the Euclidean space, because direction and magnitude are not the only predicates of vectors. The concept of vector fields does this. It is left to the reader to think of other examples of intensional and extensional equivalence in mathematics.
In the field of programming and computer science, this piece of Python code:
for x in range(0,10):
print(x)
is intensionally equivalent to this piece:
x = 0
while True:
print(x)
x +=1
if x == 10: break
because it is interpreted as the same sequence of events. The former way of writing it is just an easier way than the latter, but they are essentially one and the same. This is a good example of the difference in the starting point that distinguishes the law of identity of the discernibles from the law of indiscernibility of the identicals. Because we made Python, we start by asserting that the two pieces of code are indeed the same; hence, no essential differences exist between them. In terms of meaning, they are both two referents that have the same reference. A piece of machine code that does the same thing would be identical to the previous pieces of code only if there was no interpreter overhead. This is an example of how the meaning might be the same, but the implementations (related to a physical object) differ.
Consider another example. Suppose that some business makes a total profit \(x\) on which a 20% flat-rate tax is due. If the business owner hires a tax expert to find some way to reduce the taxes, and the expert asked for a percentage of 1% of the total business profit, the business owner would end up with the same net profit if that expert could save the business only what is equivalent of 1% of \(x\). The net profits in both cases will be extensionally equivalent in terms of value, but the details are considerably different; i.e. the two cases are not identical.
Because mathematics consists of abstract concepts that we build in the mind, we can often be certain that some concepts are intensionally identical to others. The detachment of such abstract concepts from physical matter means that intensional equivalence will always be valid. It is often not crucial to distinguish between extensional and intensional equivalence in mathematics, but sometimes the distinction is necessary, especially when we apply mathematics to real-world situations, thus giving it meaning that is tied to physical objects. Consider the mathematical concept of a fraction. A tenth of one is always so under all circumstances, and ten tenths make a whole. However, there is no such thing as one tenth of a hydrogen atom such that combining ten of those tenths results in one hydrogen atom (or at least that's the best we know.)
In mathematics, the law of indiscernibility of the identicals states that for all entities \(x\) and all entities \(y\), if \(x\) is identical to \(y\), then for all predicates \(P\), it is true that \(P(x)\) if and only if it is true that \(P(y)\). \[ \forall x \, \forall y \, (x = y \rightarrow \forall P \, [P(x) \leftrightarrow P(y)]) \] The equivalence relation meant by the expression ‘is identical to’ implies reflexivity, symmetry and transitivity. The law of the identity of the indiscernibles is stated in second-order logic as: \[ \forall x \, \forall y \, (\forall P \, [P(x) \leftrightarrow P(y)] \rightarrow x=y ) \] It is evident from above how the starting point of assertion makes the difference between the two laws. It is also evident how knowing all predicates \(P\) for entities \(x\) and \(y\) is necessary for concluding that \(x\) is identical to \(y\). The converse of the law of indiscernibility of the identicals, sometimes called ‘the law of dissimilarity of the diverse,’ in terms of second-order logic is: \[ \exists x \, \exists y \, (x \neq y \leftarrow \exists P \, [P(x) \nleftrightarrow P(y)]) \] which states that there exists at least one entity \(x\) and one entity \(y\) such that if \(x\) is nonidentaical to \(y\), it is necessary that at least one predicate \(P\) of \(x\) has a different truth value from the same predicate of \(y\). The converse of the law of identity of the indiscernibles in terms of second-order logic is: \[ \exists x \, \exists y \, (\exists P \, [P(x) \nleftrightarrow P(y)] \leftarrow x \neq y) \] which states that there exists at least one entity \(x\) and one entity \(y\) such that if there is at least one predicate \(P\) of \(x\) that has a different truth value from the same predicate of \(y\), it is necessary that \(x\) and \(y\) are nonidentical. This is another way to rephrase the law of dissimilarity of the diverse. Combining them together, we get a combined expression for this law, which is: \[ \exists x \, \exists y \, (x \neq y \leftrightarrow \exists P \, [P(x) \nleftrightarrow P(y)]) \] meaning basically that two entities can be nonidentical if and only if there exists at least one predicate that is different between them.
Fifth: Principle of sufficient reason
This principle, fundamental as it is to the thought process in general, has limited connection to mathematics. A form of the principle is that every conclusion has to have sufficient reason; i.e. justification. Other forms of the principle discuss the relation of cause and effect. This is irrelevant to the field of mathematics. Discussing this principle in depth is beyond the scope of this article, and is indeed worthy of a separate article. The most controversial form is that discussing cause and effect, which has no consequence on mathematics. I doubt that any sane person, especially if they are interested in mathematics, would argue that conclusions are acceptable with no reasoning.
The only distinction I would like to make in this context is the difference between a conclusion and a belief. The former must be justified, while the latter is a personal choice. Mathematics contain no beliefs; only conclusions. In everyday life, people believe different things; some of which is claimed to be based on purely subjective personal knowledge that is impossible to transfer to others. I do not have any objections to holding any ideas, as long as they are not in contradiction with the other ideas that a person holds, i.e. all concepts in one mind are coherent, because of the law of non-contradiction.
I fully acknowledge the following:
- that our ability to know is limited; we cannot possibly know everything, especially about physical objects,
- that some of our knowledge is purely subjects; it cannot be transferred from one mind to another in any way,
- that the absolute truth, albeit existing, is unattainable because of our limitations,
- that the truth is exceedingly complex; we may differ in our points of view because we may have different perspectives of the absolute truth,
- that no sane intelligent being is capable of consciously holding two conflicting concepts.
For those reasons, I do not claim to know the absolute truth, but I claim to have the mental faculties that are necessary to search for the truth and examine the various concepts for validity. This has to be done with high attention to the precise meaning. Being limited in abilities, I invite you to help me understand better with your feedback, aiding me with the abilities of yours that I do not have.